之前提到形成一個具連乘證明的多項式，當獲得到相關的多項式後，究竟可以做什麼呢?
其實這可以用來實現一個Multiset等價證明。

證明Multiset等價

首先可以假設有2個不同的向量，其中一個向量是另一個向量的亂序排列，即雖然兩個向量不同，但它們所包含的元素是一樣的。
不過我們又可以怎樣證明到它們是集合無序的一個等價向量，接下來會教大家怎樣去證明它。

在講解正確的方法前，也想講一下不能夠證明的情況，好讓大家可以注意。
第一個情況是依次枚舉其中一個向量中的每個元素，及需要證明它的所有元素是屬於另一個向量，即同時也存在另一個向量，它的所有元素是跟這個向量所擁有的元素相同，只是在次序上會有所不同。不過會存在一個問題，就是沒辦理處理向量中有2個或以上相同元素的情況，換言之就是不支持一個多重集合(Multiset)的情況。假如向量A: {1,2,3,3} 就是一個具有多重集合(Multiset)的向量，而它是跟向量B: {1,2,2,3}是不相等的，跟向量C: {1,1,2,3}也是不相等的。
第二個情況是利用連乘關係，將兩個向量中的所有元素都進行連乘，然後根據向量的連乘值來判斷兩個向量是否相等。同樣在這個例子也是會出現問題的，因為就算連乘值是相等，其實也不能表示兩個向量是具有相同的元素。假如向量D: {3,8} 和向量E: {4,6}是具宥相等的連乘值，不過事實上它們所包含的元素是不相等的。所以也是不能夠利用連乘關係是做相關證明。

因此，需要一個多項式來滿足證明關係，可以假設存在一個向量Q，它是一個多項式q(X)的根集合，所以對向量中的任何元素，都可以滿足到q(X)=0的情況。所以會有以下的多項式:

換言之，如果有一個多項式p(X)是與q(X)相等，就必然會有相同的根集合: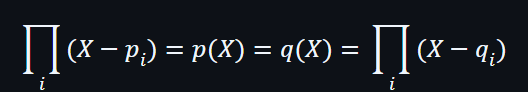

在這個關係中，就可以證明到

再進一步解釋，可以透過Schwartz-Zippel來進行測試，證明者進行測試時，要向驗證者取得一個隨機數β，
當證明者獲得隨機數β後，可以利用以下等式去證明兩個向量是否在多重集合之下相等: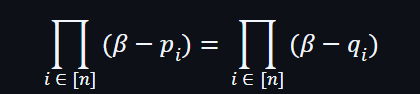

然而要進行驗證，還需要利用到連乘證明，所以要再加上一個輔助向量作為一個累加器來進行連乘證明。
通過連乘關係轉換為多個單乘以證明兩個向量的關係，當兩個向量是具有相等關係時，可得出以下公式: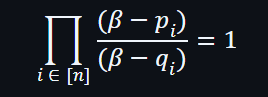

因此到了這一步就是已經證明到兩個向量存在一個Multiset等價。